磨课,是集各位老师的备课、授课精华,集自己平时积累的教学经验反复推敲、反复讲解的过程。磨课的特点是:同课异构,各位专家老师给出教学诊断。 一个“磨”字道出了其中的反反复复、斟酌修改和耗费的大量汗水!一个“磨”字,犹如侠客十年磨一剑、修炼得道一样,道出了一节成功好课的艰辛和不易!
线性代数是理工科重要的基础课程,课程教学涉及的人数多。与其他基础课程相比,这门课程概念多,内容相对复杂,研究对象也更为抽象。学生学习起来容易入门但是深入较难,这让同学们在学习线性代数的过程中容易产生畏难情绪甚至半途放弃。因此,在教学中适时的激励学生、调动他们对《线性代数》课程学习的兴趣,是帮助同学们顺利完成该课程学习的关键。我认为:适时的介绍数学家刻苦努力、进取创新的精神,融数学发展史、数学文化史、课程思政教育于线性代数课堂教学可有利的促进线性代数课程的教学。具体而言,实际教学可以从以下几个方面来打磨:
1. 课程教学引入生活案例,摈弃数学无用论
一些学生在高中阶段疲于解题技巧的训练,步入大学阶段接触的数学课程又是抽象难懂,所以对数学类课程内心存有畏难情绪,心里暗示作用凸显。另外,因为大学阶段数学类课程都开设在大一、大二阶段,他们暂时未接触过相关专业课程,无法建立数学课程与其他专业课程的联系,认为这类课程并不实用,提不起学习的兴趣。
行列式和矩阵是初学线性代数这门课程的重点和难点,也是学习这门课程的起点。在讲解二阶、三阶行列式时,如果引入三阶行列式:
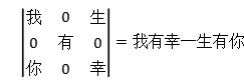
这个行列式称为爱情行列式。
我想通过讲解这个行列式,同学们会对行列式的学习充满好奇,同时也能清楚地认识到行列式在生活中无处不在,从而提高学习《线性代数》课程的兴趣。
现代社会,特别是大学生格外讲究美,注重饮食健康问题。因此减肥也就成了很多年轻人喜欢探讨的问题。众所周知每一种食物都有它的营养素含量,比如:卡路里、蛋白质、碳水化合物等含量,我们可以根据营养素利用矩阵建立健康饮食的模型,这个模型简单易建,容易理解,同学们也会比较感兴趣并增加学习积极性。
国家建设涉及到工业、农业、国防、科技等各个领域,而每一个领域都有不同的层面,据此,我们也可以利用矩阵建立模型。同学们会感到今天的学习与祖国的建设密切相关,从而增强学习的动力、增强主人公的感觉。
2. 融数学史于课堂教学,培养学生们的科学精神,激发爱国情怀
行列式、矩阵、向量是线性代数中三个基本的计算单元。线性代数教学一般利用高斯消元法解线性方程组而引入行列式的概念及应用。我们可以引导学生们回顾数学史,以加深对这些内容的理解。告诉同学们有史书记载,行列式是由莱布尼茨和日本数学家关孝和发明的,而后克莱姆在其著作《线性代数分析导论》中对行列式进行了系统的阐述,并给出了利用行列式解线性方程组的方法——克莱姆法则。 我国东汉初年成书的《九章算术》中记载有求解线性方程组的方法,其计算步骤中的偏乘、直除就类似于今天初等变换的倍法变换和消法变换。告诫同学们,前辈们发明创造的知识今天我们来学习,没有理由不学好、学不好!
3. 将数学文化引入教学课堂,培养科学审美能力、提高同学们的美学修养
数学家伽利略说:“自然这部巨著是用数学语言写成的”。数学不仅是一种学术形态,还是一种文化,它用自己特有的语言和符号解释着自然界的规律。线性代数的内在美体现在简洁、规范;外在美体现在应用性强,便于操作。
同样以行列式为例,行列式是线性方程组求解过程中提出的一种速记表达式。n阶行列式的定义是
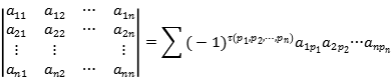
这个表达式抽象难记,我们可以这样引导:
n阶行列式的展开式中每一乘积项都来自于不同的行和不同的列,即从行来看,每一行都有且仅有一个元素被取到,从列来看,每一列也都有且仅有一个元素被取到,这体现了均衡性美;再深入引导,对角行列式的定义是对角线上元素不全为0,其他元素全为0,这从形式上来看,对角行列式特点就是关于主对角线对称,它体现了一种对称美; 计算高阶行列式常用方法的是化一般行列式为三角形行列式再计算,实质是一个化繁为简的过程,这体现了简洁之美。矩阵是线性代数的核心内容,矩阵是将元素排成行、列的数表,有了这个概念,元素不再显得杂乱无章,这体现了线性代数的整洁之美。在n阶方阵里还有一类行列式不等于0的方阵称为奇异矩阵,这是矩阵的奇异之美。通过这样的讲解应该说把枯燥难学的数学内容和事物的美学联系了起来,会极大的调动同学们的学习兴趣和积极性。
作为一名高校教师,在课堂上为同学们讲好课、讲精品课是天职。为了讲好课,课前进行必不可少的课程研读和精心打磨,是教书育人、对学生负责的具体体现。怎样上好《线性代数》这门课?怎样融思政教育于《线性代数》课程教学?怎样激发同学们的学习积极性、发挥同学们的主观能动性,提高知识的应用能力?怎样培养同学们的科学审美能力,树立正确的人生观、世界观、价值观值得我们认真推敲,打磨。




